从《社交网络》以及美女排名系统看问题

大概是2个月前看的这部电影,没有过多关注拍摄手法、演技等电影元素,关注的是Jesse Eisenberg对Mark的人物演绎。人和人是有差距的,这点我很赞同。那么,我和Mark之间的差距在哪?
来分析下:
- Mark是一个Geek(褒义的),我是一个伪Geek。
- Mark对技术狂热,热到可以不吃不睡以及禁欲,我对技术热爱,爱到可以不吃晚睡但不会禁欲。
- Mark可以心无旁骛的钻研,我可以左顾右盼的学习。
是的,差距就是这样来的,可能我较Mark好的就是,我对衣着的品位还是好一点,毕竟Mark去年被英国时尚杂志《Esquire》评为十大着装品位最差男人之一嘛,哈哈,玩笑话……
来说说正事吧,一直对Mark的Facemash对女孩评分的算法感兴趣,今天琢磨了一下,写写心得体会。
该排名系统出自Elo Rating System,根据维基百科的介绍:
The Elo rating system is a method for calculating the relative skill levels of players in two-player games such as chess. It is named after its creator Arpad Elo, a Hungarian-born American physics professor.
Elo rating system是一个用于计算两人对战模式中参赛者相对技术水平的方法,如象棋。是根据它的创造者匈牙利裔美国物理学家Arpad Elo命名的。
The Elo system was invented as an improved chess rating system, but today it is also used in many other games. It is also used as a rating system for multiplayer competition in a number of computer games,[1] and has been adapted to team sports including association football, American college football and basketball, and Major League Baseball.
这个系统最初设计用来改善国际象棋排名系统,但是现在也用在其它比赛中。同样也可以用在多人竞技的电脑游戏的排名系统,也被团队运动所采纳,如足球比赛、美国大学足球和篮球比赛和棒球联盟比赛。
Elo假设:
1.参赛选手在每次比赛中的表现成正态分布;后来普遍认为Logistic分布更为合理(抱歉,由于专业和知识限制,无法解释以及理解Logistic分布)
2.在一局比赛中,赢的一方被认为表现较好,输的一方被认为表现较差;若平局,则双方表现大致相当。虽然这个假设貌似很稀松平常。
算法如图:

Ea为选手A的期望表现,Ra为选手A当前的等级分排名。
当选手A和B进行比赛时,可根据公式算出两选手的期望表现。
Ea + Eb=1
胜方得1分,负方得0分。(在电影中,不会出现平局)
如果选手的表现比期望要好,那么此选手的排名应该上升。相反,若表现不如期望,则排名会下降。
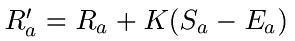
Sa为选手A本局的得分(1或0),Ra为选手A的期望表现。K为常数,在大师级象棋赛中通常取16。得到的Ra’为选手本局比赛后的等级分排名。
初始可认为每个人的等级分排名为0。
第一局是A和B进行比赛。此时Ra=Rb=0,Ea=Eb=0.5。
假设本局A胜B负,则A的得分为1,B的得分为0。
Ra’=0+16*(1-0.5)=8
Rb’=0+16*(0-0.5)=-8
上面的算法过程主要是转载的豆瓣网友的,原文请看参考资料。
通过Mark创建Facemash给我的启发很大:第一,数学非常重要。第二,其实看似很高深的东东,放到生活中就会那么有趣。不过,前提得是你知识的深厚与渊博,这也是我考研的一个目的,尽管落榜了T_T。
参考资料: