一、问题描述

有n个元素，需要随机选择m个，且要保证每个元素被选的概率相同。

二、解决思路

1）解法一

拿这题问朋友的时候，很多人都是说：“一个m长度的for循环，取m次random。”

这个方法看似可以，简单方便，代码也一目了然：

1
2
3
// random() -> (0,1)
for i in [0, m):
    results[i] = data[random()*(n-1)]

但是，这段代码有什么问题吗？结果集中会不会出现重复的结果呢？既然是随机的，那肯定就有可能重复，如何消重就得看解法二了。

2）解法二

要消重的话，就需要将已经选择的元素剔出，不进入下一次迭代过程。这个就和中国古代的“抓阄”是一个概念了，用高中知识解释就是“古典概率模型”——在有限多个基本结果、每个结果出现的可能性相同的条件下，先选与后选概率相同。

将已经选择的元素剔出看似很方便，直接删除即可。但是数据集采用数组形式存储，删除的时间复杂度为线性，有人又说可以改成链表，但是链表存储查找又是线性时间了。那么我们能做的就是不删除元素，只是改变一下它的位置：将已选择的元素移到数组末尾。如下图：

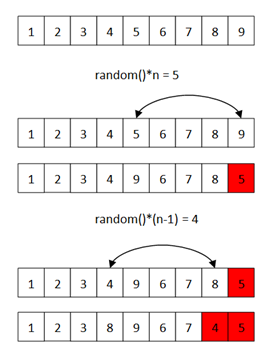
image

代码如下：

1
2
3
4
5
// random() -> (0,1)
tmp := n-1;
for i in [0, m):
    swap(data, random()*tmp, tmp);
    tmp–;

题外话：以上问题源自实际编码中，同时在编程珠玑 II中也有提到，不过书中所提到是现实生活问题：N个地区，随机选择M个做样本。书中提到了一个很有趣的解法：“将N个地区名字打印出来，剪成均等的字条，放入纸篓摇乱，抓取M条。”作者称之为haha!算法，的确，看到这个算法我也哈哈大笑了很久。有时候，我们如果打破我们的概念壁垒，换一种思维思考问题，是一种解法更是一种乐趣。

三、问题升级

问题一升级，就到了Google的经典面试题了：给你一个长度为N的链表。N很大，但你不知道N有多大。你的任务是从这N个元素中随机取出k个元素。你只能遍历这个链表一次。你的算法必须保证取出的元素恰好有k个，且它们是完全随机的（出现概率均等）？

四、升级问题解法

不知道N的长度，就不满足古典概型的有限个基本问题的要求。如题目没要求只能遍历一遍，可否求出长度再转换成古典概型呢？怕也不行，如果数据是动态增加的，两次遍历依然无法解决问题。

那么问题就转换成蓄水池抽样（Reservoir Sampling）问题了。算法描述如下：

1）先选择前k个元素，放入结果集中；

2）从k+1开始，取[1, k+1]的random，如果得到的随机数小于k，就替换掉结果集中的相应元素；

3）重复第2步，直到迭代完毕。

伪代码：

1
2
3
4
5
6
7
8
// random() -> (0,1)
for i in [0, n):
    if i < k then: // 将前k个元素放入结果集中
        results[i] := data[i];
    else:
        tmp := random() * i;
        if tmp < k then:
            swap(results, tmp, data, i); // 交换结果集与数据集的元素

证明1：

1）前k个被选中的概率均为1；

2）第k+1个元素被选中概率为k/k+1，结果集中的元素没被剔出的概率为： 1-p， p = （k / k+1）×（1 / k）。k / k+1为第k+1被选中的概率，1 / k为不幸被剔出的概率。综上，结果集中元素没被剔出的概率也为k / k+1；

3）归纳法，即可证明。

证明2：

同样也可以这样证明，元素a被选中的概率为：

被选中的概率×（后面元素没被选中 + 后面元素被选中 × 没被替换的概率）

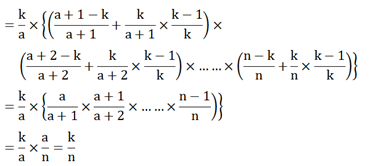
image

证明2简明扼要啊！

五、总结

其实没啥好总结的，上面所提到仅仅只是概率运用的很小一部分。对概率理解还是得从古典概率模型出发，一般情况下，书上将概率算法大致分为四类：数值概率算法、蒙特卡罗（Monte Carlo）算法、拉斯维加斯（Las Vegas）算法和舍伍德（Sherwood）算法，我也没想通上面的是属于上面四种的哪一种，或许哪种都不是，算法嘛，思想在即可，不必纠结于概念。