1、简介

在某些应用中，会将n个不同的元素分成一组不相交的集合（disjoint）。不相交的集合有两个重要的操作，即找到给定的元素所属的集合（find）和合并两个集合（union）。为了更好的支持这两种操作，就出现了并查集（Disjoint-Set or Union-find set）。

并查集保持了一组不相交的动态集合，每个集合通过一个代表来识别，代表即集合中的某个成员。哪个成员被选中无所谓iwom关心的是如果寻找某一动态集合的代表两次，并且在两次寻找之间不修改集合，两次得到的答案应该是一样的。

2、基本操作

它主要涉及两个基本操作，分别为：

  • Union-Set(x, y)：合并两个不相交集合

  • Find-Set(x)：判断两个元素是否属于同一个集合

还需要另外一个基本操作，即：

  • Make-Set(x)：新建一个集合，唯一的成员也是代表就是x

3、实现方法

现有不相交集合：{1, 3, 7}，{4}，{2, 5, 9, 10}，{6, 8}

1）用编号最小的元素标记所在集合

{1, 3, 7}，{4}，{2, 5, 9, 10}，{6, 8}

2）定义一个数组set[1…n]，其中set[i]表示元素i所在集合

clip_image002

3）find操作

1
2
find(x):
     return set[x];

4）Union操作

1
2
3
4
union(x, y):
    for k in [0, n): // 遍历所有集合，更新其中一个集合的代表
        if (set[k] == find(a)):
            set[k] := find(b);

4、实现分析

上面实现很简单，find操作只需要返回其代表即可，时间复杂为O(1)。但是Union操作则需要修改其中一个集合所有的代表，同时由于是用的数组存的，元素为数组的索引，必须要遍历所有元素才可以修改，时间复杂为O(n)。要优化操作，就必须优化数据结构。

5、优化

1）链表

每个集合建立一个链表，有头尾指针，头结点为代表。所有结点都添加了指向代表的指针。

很容易知道，find操作时间复杂度为O(1)，合并只需要将较小的集合添加到另一个集合的后尾，再更新代表即可，时间复杂度也为O(n)，与数组相比，在时间上优化了一点点。

2）有根树

并查集目前最好的实现是用有根树，即建立一个森林，每棵树是一个集合，树根元素就是代表，每个结点存储指向其父亲结点的指针（而不是指向子结点的指针）。

可执行三种不相交集合操作：

  1. Make-Set：创建一颗仅包含一个结点的树；
  2. Find-Set：查找可以描述为找两个元素各自的根，判断其是否相等。实现中需要沿着父结点指针一直找下去，直到找到树根为止。（时间复杂度O(n)）
  3. Union-Set：并集可以描述为把一棵树接到另一个棵树的根结点上，并更新某颗树的代表。（时间复杂度O(n)）

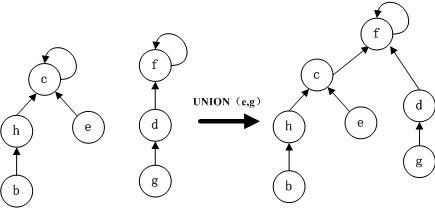
clip_image003

其实这个与链表来说，性能没有本质上的提高。合并也需要更新结点代表，且如果树构造的时候，构造了一颗线性链的树，查找复杂度也提高了。对其进行优化，有两种策略：

a. 按秩合并（union by rank）

秩（Rank）就是一颗树的结点数，即使包含较少结点的树根指向包含较多结点的树根。

b. 路径压缩

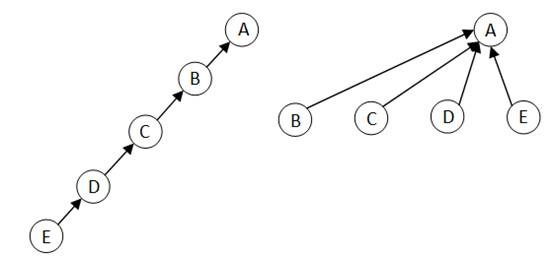
clip_image005

如上图，使查找路径上的每个结点都直接指向根结点。简单而有效。

6、小结

在实现中，并查集均是使用有根树结合按秩合并和路径压缩来实现。按秩合并提高了Union-Set操作效率，而路径压缩提高了Find-Set操作效率。

空间复杂度为O(N)，建立一个集合的时间复杂度为O(1)， N次合并M查找的时间复杂度为O(M Alpha(N))，这里Alpha是Ackerman函数的某个反函数，在很大的范围内（人类目前观测到的宇宙范围估算有10的80次方个原子，这小于前面所说的范围）这个函数的值可以看成是不大于4的，所以并查集的操作可以看作是线性的。具体证明得参加《算法导论》。

并查集常作为另一种复杂的数据结构或者算法的存储结构。常见的应用有：求无向图的连通分量个数、最近公共祖先（LCA）、最小生成树等。

参考资料：

《算法导论》，第二十二章

董的博客：数据结构之并查集