一、定义说明

动态规划（Dynamic Programming）是通过组合子问题的解而解决整个问题的。分治法算是是将问题划分成一些独立的子问题，递归地求解各子问题，递归地求解个子问题，然后合并子问题的解而得到原问题的解。而动态规划与此不同，它是用于子问题不是独立的情况，就是各子问题包含公共的子的子问题。

动态规划常用于求最优解问题，此类问题可能有很多可行解，每个解都有一个值，而我们希望找到一个最优（最大、最小）值的解。需要注意，这样的问题可能有多个最优解，但是我们只求解一个。

动态规划算法的设计分为如下4个步骤：

  1. 描述最优解的结构；
  2. 递归定义最优解的值；
  3. 按自底向上的方式计算最优解的值；
  4. 由计算出的结果构造一个最优解。

二、简单示例

斐波那契（Fibonacci）数列。相信所有大学生都对这个名字不会陌生，大计基（大学计算机基础）课上老师会给大家一个这样的公式：

f(n) = f(n-2) + f(n-1); f(0) =0, f(1) = 1

同时，老师就会给一个递归的解，几行代码了事。期末或国家计算机考试的时候，写出递归解就算过关了。但对于我们程序猿来说，可不是这么回事了，递归算f(20)都算不出来。

不知道拿Fibonacci说事合理不合理，因为Fibonacci数列不存在最优不最优，我们姑且算求得答案算最优解吧。

动态规划有两个要素：最优子结构与重叠子问题。

  • 最优子结构要素：如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构要素。
  • 子问题重叠要素：子问题重叠要素是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。

Fibonacci数列满足最优子结构，那子问题重叠呢？f(n-1)、f(n-2)均要用到f(n-3)的解，但是每次都要重复计算一次，所以也满足子问题重叠性质。

已经描述了Fibonacci的最优解结构，公式也就是其递归解，现在需要做的就是自底向上计算最优解了，伪代码如下：

1
2
3
4
f[] := new bigint[n];
f[0] := f[1] := 1;
for i in [2, n):
     f[i] := f[i-1] + f[i-2];

构造出的最优解就是上述代码中的f(n)了。动态规划利用了子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。

三、经典例子

接下来汇总一些经典的动态规划问题，但是只给出状态转移方程（递归解）和伪代码。

1）01背包问题

有N件物品和一个容量为W的背包。第i件物品的重量是w[i]，价值是v[i]。求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量，且价值总和最大。为啥叫01背包呢，因为每个物体就一件，放就是1不放就是0。

子问题为V[i][w]，定义为：前i件物品恰放入一个容量为w的背包可以获得的最大价值。

状态转移方程：

V[i][w] = MAX{V[i-1][w], V[i-1][w-w[i]]+v[i]}

其中，V[i-1][w]代表第i件物品没有加入到背包中（为0），V[i-1][w-w[i]]+v[i]表示第i件物品加入了（为1），在01中取最大值。

伪代码：

1
2
3
4
V[][] := new int[n][W]
for i in [1, n):
    for w in (W, w[i-1]]: // 保证w-w[i-1]不越界
        V[i][w] := MAX{V[i-1][w], V[i-1][w-w[i]]+v[i]}

上面的时间复杂度为O(nW)，空间复杂度也为O(nW)。我们可以压缩一下空间，因为我们只需要袋子装满没有，装满后的价值是多少，设V[w]：在w重量下，袋子中物品的最大价值。

状态转移方程：

`V [w] = MAX{V[w], V[w-w[i]]+v[i]}``

伪代码：

1
2
3
4
V[]:= new int [W+1]
for i in [0, n):
    for w in [W, w[i]-1]: // 保证w-w[i-1]不越界
        V[w] := MAX{V[w], V[w-w[i]]+v[i]}

2）最长公共子序列（Longest Common Sequence）

求两数组相同的最长子序列，子序列可以不连续的。状态转移方程：

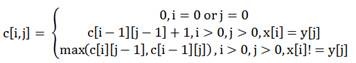
clip_image002

c[i][j]表示在字符串x的i位前与字符串y的j位前最长公共子序列。很容易理解，如果一个x[i]、y[j]相等，c[i-1][j-1]加1，不等的话，c[i][j]等于c[i-1][j]、c[i][j-1]中较大的数。

伪代码：

1
2
3
4
5
6
7
8
9
c[][] := new int[len(x)][len(y)]
for i in [0, len(x)):
    for j in [0, len(y));
        if i==0 || j==0 then:
            c[i][j] :=0;
        else if x[i] == y[j] then:
            c[i-1][j-1] += 1;
        else:
            c[i][j]:= MAX{c[i][j-1], c[i-1][j]};

3）最长递增子序列（Longest Increase Sequence）

求一个一维数组（N个元素）中最长递增子序列的长度。状态转移方程：

LIS[i+1] = MAX{1, LIS[k] +1}, array[i+1] > array[k], for k in [0, i]

伪代码：

1
2
3
4
5
6
L[] :=new int[len(array)];
for i in [0, len(array)):
    L[i] := 1 // 初始默认为1
    for j in [0, j):
        if array[i] > array[j] && L[j] +1 > L[i]:
            L[i] = L[j] +1;

四、小结

以上整理自算法导论、编程之美;，要掌握动态规划主要是理解两个要素：最优子结构和重叠子问题。要懂得找到一个好的表格来装子问题，将大问题逐步简化，直到得到状态转移方程。表格即子问题最优解，如背包问题：V[w]为背包重量为w的时候最大价值；LCS问题：c[i][j]为x[0, i]、y[0, j]的最大子序列；LIS问题：L[i]为array[0, i]的最大递增序列。

但要完全掌握动态规划仅靠以上几道经典问题是不够的，需要不断思考、分析、实践，才可逐渐掌握这一算法分析设计方法。以上经典问题的解答也是经典的，还有许多需要优化以及修改的地方，但不写在博客里了，有兴趣的可以参考相关书籍，也欢迎留言讨论。