一、定义说明

回溯法是一个即带有系统性又带有跳跃性的搜索算法，它在问题的解空间树中，按深度优先搜索策略，从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时，先判断该结点是否包含问题的解。如果肯定不包含，则跳过对该结点为根的子树的搜索，逐层向其祖先结点回溯；否则，进入该子树，继续按深度优先策略搜索。

回溯法是设计递归过程的一种重要方法，它的求解过程实质上是一个先序遍历一颗状态树的过程，只是这一棵树不是遍历前预先建立的，而是隐含在遍历过程中。

二、简单示例

经典回溯的例子是求n个元素的幂集，幂集简单点说就是n个元素的全组合再加上空集，它的解空间树（状态树）如下：

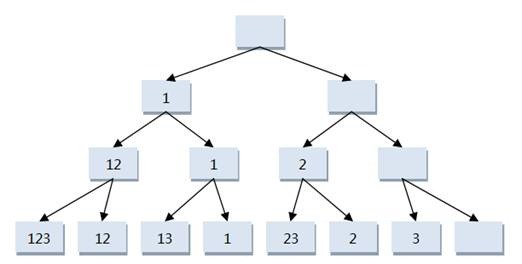
clip_image002

上面的树是一颗满二叉树，树中每个结点的状态都是求解过程中可能出现的状态（即解）。递归过程可以简单理解为对n个元素的0、1取舍，伪代码如下：

1
2
3
4
5
def powerset(i : int):
    if i > n Then: print
    else:
        取第i个元素（1）; powerset(i+1);
        舍第i个元素（0）; powerset(i+1);

三、问题说明

很多问题用回溯法求解时，描述过程的树不是一颗满二叉树，这类问题在求解之前需要确定问题的约束函数：“约束函数是根据题意定出的，通过描述合法解的一般特征用于去除不合法的解（剪支），从而避免继续搜索出这个不合法解的剩余部分。因此，约束函数是对于任何状态空间树上的节点都有效、等价的。”

以四皇后问题为例，剪支后的状态树如下：

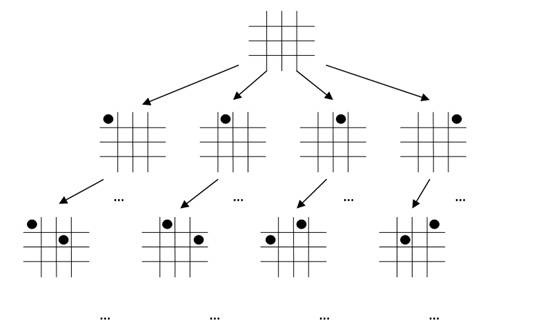
clip_image004

伪代码如下：

1
2
3
4
5
6
7
def trial(i : int):
    if i>n Then: print
    else:
        for j in [0, n):
            在(i, j)处放置棋子;
            if 布局合法 Then: trail(i+1);
            拿走(i, j)处的棋子

4、浅谈搜索

上面所说的回溯法在算法导论中没有提到，觉着有些奇怪，但是仔细一想，好像又不那么奇怪。毕竟，回溯法是一种建立查找树、遍历树的递归应用算法，这些基础的知识在算法导论中均有详细解释，书中没单独辟章说明也不足为奇了。

和朋友@烟雨华年讨论这个的时候，他提到：将整个搜索状态树中的每一个结点看作一种状态，搜索一般是求一种状态到指定状态有没有可行的变化，或者最佳的变化。个人觉得这句概括得还是挺到位的，大部分搜索都是检索从初始状态（状态树的根）到某个状态的变化，而可行的变化即验证是否存在解，最佳的变化即求最优解。

说到这里又不得不说搜索两种最基本的方式，深度优先搜索（DFS）和广度优先搜索（BFS），网络上都是简单的描述一些，并没对它们的运用有一个很好的解释，那么这两种方式如何更好的运用呢？

简单点说，就是验证最优解用DFS，搜索最优解——解空间小用BFS。

1）DFS有着内存需要相对较少的优点，可以利用栈在有限的空间内遍历所有的解，如前面提到的回溯法；

2）BFS类似于树的分层遍历，有限空间的情况下无法使用。但是由于它分层的特性，可以保证当前搜索到的解都是最优解，可以不用完全遍历完解空间的情况下，找到最优解。如最短路径算法。

网上还有一个有趣的说法：一个行不通就用另外一个！哈哈，想图省事的话，找一些模拟数据来跑一圈，是驴是马很快就可以见分晓啦！

五、结束语

搜索，算法中最重要的一个环节，以上仅是对它的粗浅认识，对其理解还有待进一步的深入。